一、填空題
1.1023456789102346[解析] 越小的數字放在越靠左的數位上得到的數字越小,但零不能放在最左邊的首數位上。故可得最小的十位數為1023456789,四舍五入到萬位為102346萬。
2.6π9π平方厘米[解析] 正方形中剪一個最大的圓,即為該正方形的內切圓。故半徑r=12×6=3(厘米),所以它的周長為2πr=2π×3=6π(厘米),面積為πr2=π×32=9π(厘米2)。
3.1710[解析] 由題干知△+2□=44(1)
3△+2□=64(2),(2)-(1)得2△=20,則△=10,從而2□=44-10,解得□=17。
4.60分鐘[解析] 由題干可知,本題的實質是求20與15的最小公倍數。因為20=2×2×5,15=3×5,所以它們的最小公倍數為2×2×3×5=60。即再遇到同時發車至少再過60分鐘。
5.21[解析] 設分母應增加x,則2+67+x=27,即:2x+14=56,解得x=21。
6.1199[解析] 略
7.y=1[解析] 與x軸平行的直線的斜率為0,又在y軸上的截距為1,由直線方程的斜截式可得,該直線的方程為y=1。
8.-1[解析] 間斷點即為不連續點,顯然為x+1=0時,即x=-1。
9.12[解析] 由f(x)=x可知,f′(x)=(x)′=(x12)′=12x-12=12x,故f′(1)=12×1=12。
10.1[解析] 因為f′(x)=3x2≥0,所以f(x)在定義域R上單調遞增,所以在[-1,1]上也遞增,故最大值在x=1處取得,即為f(1)=1。
二、選擇題
1.C[解析] 2能被2整除,但它為質數,故A錯誤。4能被2整除,但4是合數而不是質數,故B錯誤。奇數都不能被2整除,能被2整除的數都為偶數。
2C[解析] 長方形有兩條對稱軸,A排除。等邊三角形有三條對稱軸,B排除。圓有無數條對稱軸,D排除。等腰三角形只有一條對稱軸,即為底邊上的中線(底邊上的高或頂角平分線)。
3.B[解析] 鹽水有5+75=80(克),故鹽占鹽水的580=116。
4.C[解析] 由2a3+326=5b9可得,a+2=b,又5b9能被9整除,可知b=4,則a=2,所以a+b=2+4=6。
5.B[解析] 如果是自然堆碼,最多的情況是:每相鄰的下一層比它的上一層多1根,即構成了以5為首項,1為公差的等差數列,故可知21為第17項,從而這堆鋼管最多能堆(5+21)×172=221(根)。
6.C[解析] 棱柱的一個側面是矩形/ 棱柱的側棱垂直于底面,而棱柱為直棱柱棱柱的側棱垂直于底面棱柱的側面為矩形。故為必要但不充分條件。
7.A[解析] 13為分數但不是有限小數,B排除。同樣13也是真分數,但也不是有限小數,排除C。43是假分數,也不是有限小數,D排除。故選A。
8.C[解析] 對f(x)=xln(2-x)+3x2-2limx→1f(x)兩邊同時取極限為:limx→1f(x)=0+3-2limx→1f(x),即3limx→1f(x)=3,故limx→1f(x)=1。故選C。
9.B[解析] 由曲線過點(1,-3)排除A、C項。由此曲線過點(2,11)排除D,故選B。y=2x3-5顯然過點(1,-3)和(2,11),且它在(x,y)處的切線斜率為6x2,顯然滿足與x2成正比。
10. B[解析] 由A與B為互不相容事件可知,A∩B=,即P(AB)=0且P(A+B)=P(A∪B)=P(A)+P(B)。故選B。
三、解答題
1.解:[112+(3.6-115)÷117]÷0.8
=[32+(335-115)÷87]÷45
=(32+125×78)÷45
=(32+2110)÷45
=185×54
=92。
2.解:設全年級總人數為x人,則
x·48%+4x=52%
解得:x=100
所以沒有參加課外活動的人數為100×(1-52%)=48(人)。
3.解:∫x1+xdx=∫x+1-1x+1dx=∫ dx-∫1x+1dx=x-ln|x+1|+C(C為常數)。
4.解:(1)zx=2xex+y+x2ex+y=(x2+2x)ex+y;
(2)zy=x2ex+y;
(3)dz=zxdx+zydy=(x2+2x)ex+ydx+x2ex+ydy。
四、分析題
參考答案:成因:沒有理解整除的概念,對于數的整除是指如果一個整數a,除以一個自然數b,得到一個整數商c,而且沒有余數,那么叫做a能被b整除或b能整除a。概念要求除數應為自然數,0.4是小數。而且混淆了整除與除盡兩個概念。故錯誤。
預防措施:在講整除概念時,應讓學生清楚被除數、除數和商所要求數字滿足的條件。即被除數應為整數,除數應為自然數,商應為整數。并且講清整除與除盡的不同。
五、簡答題
參考答案:小學數學概念的形成過程主要包括(1)概念的引入;(2)概念的形成;(3)概念的運用。
例如:對于“乘法分配律”的講解:
(1)概念的引入:根據已經學過的乘法交換律,只是對于乘法的定律,在計算時,很多時候會遇到乘法和加法相結合的式子,如(21+14)×3。
(2)概念的形成:通過讓學生計算,歸納發現乘法分配律。
比較大小:①(32+11)×532×5+11×5
②(26+17)×226×2+17×2
學生通過計算后很容易發現每組中左右兩個算式的結果相等,再引導學生觀察分析,可以看出左邊算式是兩個數的和與一個數相乘,右邊算式是兩個加數分別與這個數相乘,再把兩個積相加。雖然兩個算式不同,但結果相同。然后就可以引導學生歸納總結出“乘法分配律”,即(a+b)×c=a×c+b×c。
(3)概念的運用:通過運用概念達到掌握此概念的目的。
計算下題:①(35+12)×10
②(25+12.5)×8
學生通過運用所學的乘法分配律會很快得到結果,比先算括號里兩個數的和再乘外面的數要快的多,從而學生在以后的計算中會想到運用乘法分配律,也就掌握了概念。
六、案例題
1. 參考答案:分析建議:張教師主要用了抽象與概括的思想方法;李老師用了教學模型的方法,先從實際問題中抽象出數學模型,然后通過邏輯推理得出模型的解,最后用這一模型解決實際問題。教師可從這方面加以論述。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
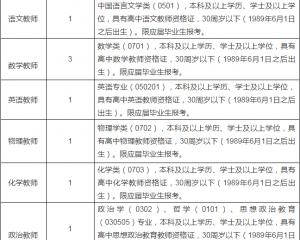 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12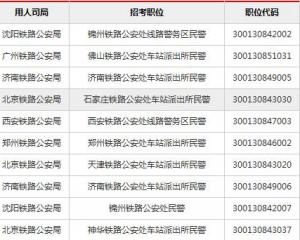 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31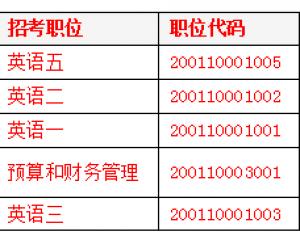 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31