經常有考生問道這個問題:“我不想在面試抽簽的時候抽到一號簽,我會緊張,希望抽到順序靠后的簽,我應該第幾個去抽會比較占便宜?”其實,抽到幾號簽都各有優劣,為此擔心毫無必要,但這背后體現的數學思想卻值得我們探討。教育專家在此進行詳解。
舉例:十二生肖一起報考天宮的公務員,結果大家并列第一,所以采取抽簽的方式來決定最終人選。名額只有一個,老鼠第一個抽,那么老鼠抽中的概率就是1/12,這個很容易理解。牛第二個抽,他的抽中的概率又是多少呢?在這里,很多學員會犯錯,他們認為一共十二個簽,老鼠抽走了一個,還剩十一個,所以牛抽中的概率應該是1/11。其實這樣理解的學員漏掉了一個條件,那就是牛要想抽中,必須是老鼠抽不中,所以牛抽中的概率應該是第一次老鼠抽不中乘以第二次牛抽中,即11/12×1/11=1/12。同樣的,老虎第三個抽,抽中的概率就是第一次老鼠抽不中,乘以第二次牛抽不中,再乘以老虎第三次抽中,即11/12×10/11×1/10=1/12。以此類推,無論是第幾個抽,抽中的概率都是1/12,所以,抽簽是絕對公平的游戲,無論你是第幾個抽,抽中的概率通通一樣。
當然,上面的例子是筆者自己的思考,公務員的考題不可能這樣出,那么大家再來看這樣一道題:
一個袋子里放有10個球,其中4個白球,6個黑球,無放回的每次抽取一個,則第二次抽到白球的概率是多少?
這道題如果是常規解法,要分類討論,先假設第一個抽中的是白球,得出一個概率1;再假設第一個抽中的是黑球,得出一個概率2,概率1和概率2的和就是我們要找的答案。這個解法相對用時較多,而且如果問你第三次甚至第四次抽中白球的概率是多少時,工作量更是倍增。如果我們使用抽簽是絕對公平的游戲這一理念,便知道無論是第幾個抽,抽中白球的概率都與第一個抽的一樣,都是4/10,便可以迅速解題了。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
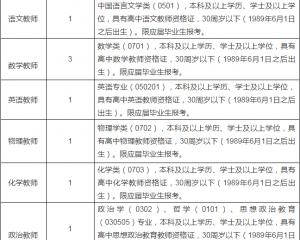 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12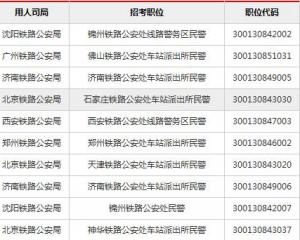 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31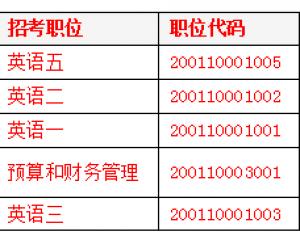 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31