知識點7:圓的基本性質
1.半圓或直徑所對的圓周角是直角.
2.任意一個三角形一定有一個外接圓.
3.在同一平面內,到定點的距離等于定長的點的軌跡,是以定點為圓心,定長為半徑的圓.
4.在同圓或等圓中,相等的圓心角所對的弧相等.
5.同弧所對的圓周角等于圓心角的一半.
6.同圓或等圓的半徑相等.
7.過三個點一定可以作一個圓.
8.長度相等的兩條弧是等弧.
9.在同圓或等圓中,相等的圓心角所對的弧相等.
10.經過圓心平分弦的直徑垂直于弦。
知識點8:直線與圓的位置關系
1.直線與圓有唯一公共點時,叫做直線與圓相切.
2.三角形的外接圓的圓心叫做三角形的外心.
3.弦切角等于所夾的弧所對的圓心角.
4.三角形的內切圓的圓心叫做三角形的內心.
5.垂直于半徑的直線必為圓的切線.
6.過半徑的外端點并且垂直于半徑的直線是圓的切線.
7.垂直于半徑的直線是圓的切線.
8.圓的切線垂直于過切點的半徑.
知識點9:圓與圓的位置關系
1.兩個圓有且只有一個公共點時,叫做這兩個圓外切.
2.相交兩圓的連心線垂直平分公共弦.
3.兩個圓有兩個公共點時,叫做這兩個圓相交.
4.兩個圓內切時,這兩個圓的公切線只有一條.
5.相切兩圓的連心線必過切點.
知識點10:正多邊形基本性質
1.正六邊形的中心角為60°.
2.矩形是正多邊形.
3.正多邊形都是軸對稱圖形.
4.正多邊形都是中心對稱圖形.
知識點11:一元二次方程的解
1.方程 的根為 .
A.x=2 B.x=-2 C.x1=2,x2=-2 D.x=4
2.方程x2-1=0的兩根為 .
A.x=1 B.x=-1 C.x1=1,x2=-1 D.x=2
3.方程(x-3)(x+4)=0的兩根為 .
A.x1=-3,x2=4 B.x1=-3,x2=-4 C.x1=3,x2=4 D.x1=3,x2=-4
4.方程x(x-2)=0的兩根為 .
A.x1=0,x2=2 B.x1=1,x2=2 C.x1=0,x2=-2 D.x1=1,x2=-2
5.方程x2-9=0的兩根為 .
A.x=3 B.x=-3 C.x1=3,x2=-3 D.x1=+ ,x2=-
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
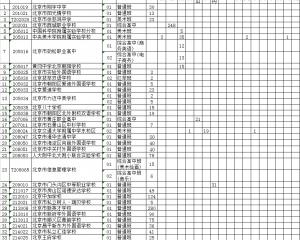 2020年北京市中招參加補錄的學校名單2020-08-19
2020年北京市中招參加補錄的學校名單2020-08-19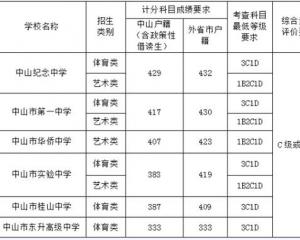 中山2018年中考錄取分數線已公布2018-08-24
中山2018年中考錄取分數線已公布2018-08-24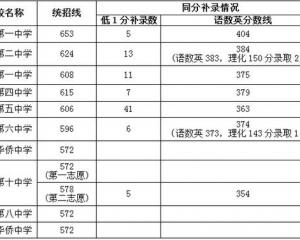 2018年福建莆田中考分數線正式公布2018-08-24
2018年福建莆田中考分數線正式公布2018-08-24 2018年遼寧本溪中考分數線已公布2018-08-23
2018年遼寧本溪中考分數線已公布2018-08-23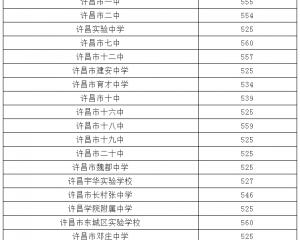 2018年河南許昌中考分數線已公布2018-08-16
2018年河南許昌中考分數線已公布2018-08-16