初一下冊數學知識點:不等式與不等式組(圖)
不等式與不等式組是初一下學期學習的第六章內容,我們整理了關于一元一次不等式的知識結構圖、有關不等式、不等式的解、不等式的解集等知識定義和經典例題。通過對本篇知識點的學習,相信同學們會結合實例體會運用不等式解決實際問題的過程,同學們加緊時間學習吧!
初一下冊數學知識點:不等式與不等式組
第九章 不等式與不等式組
一、目標與要求
1.感受生活中存在著大量的不等關系,了解不等式和一元一次不等式的意義,通過解決簡單的實際問題,使學生自發地尋找不等式的解,會把不等式的解集正確地表示到數軸上;
2.經歷由具體實例建立不等模型的過程,經歷探究不等式解與解集的不同意義的過程,滲透數形結合思想;
3.通過對不等式、不等式解與解集的探究,引導學生在獨立思考的基礎上積極參與對數學問題的討論,培養他們的合作交流意識;讓學生充分體會到生活中處處有數學,并能將它們應用到生活的各個領域。
二、知識框架
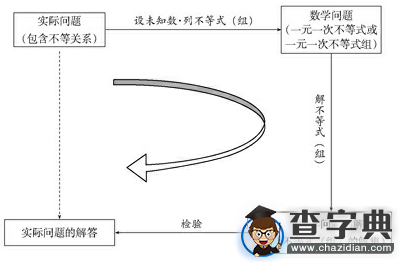
三、重點
理解并掌握不等式的性質;
正確運用不等式的性質;
建立方程解決實際問題,會解"ax+b=cx+d"類型的一元一次方程;
尋找實際問題中的不等關系,建立數學模型;
一元一次不等式組的解集和解法。
四、難點
一元一次不等式組解集的理解;
弄清列不等式解決實際問題的思想方法,用去括號法解一元一次不等式;
正確理解不等式、不等式解與解集的意義,把不等式的解集正確地表示到數軸上。
五、知識點、概念總結
1.不等式:用符號"<",">","≤","≥"表示大小關系的式子叫做不等式。
2.不等式分類:不等式分為嚴格不等式與非嚴格不等式。
一般地,用純粹的大于號、小于號">","<"連接的不等式稱為嚴格不等式,用不小于號(大于或等于號)、不大于號(小于或等于號)"≥","≤"連接的不等式稱為非嚴格不等式,或稱廣義不等式。
3.不等式的解:使不等式成立的未知數的值,叫做不等式的解。
4.不等式的解集:一個含有未知數的不等式的所有解,組成這個不等式的解集。
5.不等式解集的表示方法:
(1)用不等式表示:一般的,一個含未知數的不等式有無數個解,其解集是一個范圍,這個范圍可用最簡單的不等式表達出來,例如:x-1≤2的解集是x≤3
(2)用數軸表示:不等式的解集可以在數軸上直觀地表示出來,形象地說明不等式有無限多個解,用數軸表示不等式的解集要注意兩點:一是定邊界線;二是定方向。
6.解不等式可遵循的一些同解原理
(1)不等式F(x)< G(x)與不等式 G(x)>F(x)同解。
(2)如果不等式F(x)< G(x)的定義域被解析式H(x)的定義域所包含,那么不等式 F(x)< G(x)與不等式H(x)+F(x)
(3)如果不等式F(x)< G(x)的定義域被解析式H(x)的定義域所包含,并且H(x)>0,那么不等式F(x)< G(x)與不等式H(x)F(x)0,那么不等式F(x)< G(x)與不等式H(x)F(x)>H(x)G(x)同解。
7.不等式的性質:
(1)如果x>y,那么yy;(對稱性)
(2)如果x>y,y>z;那么x>z;(傳遞性)
(3)如果x>y,而z為任意實數或整式,那么x+z>y+z;(加法則)
(4)如果x>y,z>0,那么xz>yz;如果x>y,z<0,那么xz
(5)如果x>y,z>0,那么x÷z>y÷z;如果x>y,z<0,那么x÷z
(6)如果x>y,m>n,那么x+m>y+n(充分不必要條件)
(7)如果x>y>0,m>n>0,那么xm>yn
(8)如果x>y>0,那么x的n次冪>y的n次冪(n為正數)
8.一元一次不等式:不等式的左、右兩邊都是整式,只有一個未知數,并且未知數的最高次數是1,像這樣的不等式,叫做一元一次不等式。
9.解一元一次不等式的一般順序:
(1)去分母 (運用不等式性質2、3)
(2)去括號
(3)移項 (運用不等式性質1)
(4)合并同類項
(5)將未知數的系數化為1 (運用不等式性質2、3)
(6)有些時候需要在數軸上表示不等式的解集
10. 一元一次不等式與一次函數的綜合運用:
一般先求出函數表達式,再化簡不等式求解。
11.一元一次不等式組:一般地,關于同一未知數的幾個一元一次不等式合在一起,就組成
了一個一元一次不等式組。
12.解一元一次不等式組的步驟:
(1) 求出每個不等式的解集;
(2) 求出每個不等式的解集的公共部分;(一般利用數軸)
(3) 用代數符號語言來表示公共部分。(也可以說成是下結論)
13.解不等式的訣竅
(1)大于大于取大的(大大大);
例如:X>-1,X>2 ,不等式組的解集是X>2
(2)小于小于取小的(小小小);
例如:X<-4,X<-6,不等式組的解集是X<-6
(3)大于小于交叉取中間;
(4)無公共部分分開無解了;
14.解不等式組的口訣
(1)同大取大
例如,x>2,x>3 ,不等式組的解集是X>3
(2)同小取小
例如,x<2,x<3 ,不等式組的解集是X<2
(3)大小小大中間找
例如,x<2,x>1,不等式組的解集是1
(4)大大小小不用找
例如,x<2,x>3,不等式組無解
15.應用不等式組解決實際問題的步驟
(1)審清題意
(2)設未知數,根據所設未知數列出不等式組
(3)解不等式組
(4)由不等式組的解確立實際問題的解
(5)作答
16.用不等式組解決實際問題:其公共解不一定就為實際問題的解,所以需結合生活實際具體分析,最后確定結果。
四、經典例題
例1當x 時,代數代2-3x的值是正數。
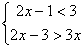
例2一元一次不等式組的解集是 ( )
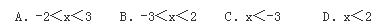
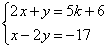
例3已知方程組的解為負數,求k的取值范圍。
例4某種植物適宜生長在溫度為18℃~20℃的山區,已知山區海拔每升高100米,氣溫下降0。5℃,現在測出山腳下的平均氣溫為22℃,問該植物種在山的哪一部分為宜?(假設山腳海拔為0米)
例5某園林的門票每張10元,一次使用,考慮到人們的不同需求,也為了吸引更多的游客,該園林除保留原來的售票方法外,還推出了一種“購買個人年票”的售票方法(個人年票從購買日起,可供持票者使用一年)。年票分A、B、C三類:A類年票每張120元,持票者進入園林時,無需再用門票;B類年票每張60元,持票者進入該園林時,需再購買門票,每次2元;C類年票每張40元,持票者進入該園林時,需再購買門票,每次3元。
(1)如果你只選擇一種購買門票的方式,并且你計劃在一年中用80元花在該園林的門票上,試通過計算,找出可進入該園林的次數最多的購票方式。
(2)求一年中進入該園林至少超過多少次時,購買A類年票比較合算。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!