考研黨們,備戰的如何,已經進入沖刺階段了,今日給大家整理了考研數學易錯的知識點:
一、幾個易混淆的考研數學概念
連續,可導,存在原函數,可積,可微,偏導數存在他們之間的關系是怎么樣的?存在極 限,導函數連續,左連續,右連續,左極 限,右極 限,左導數,右導數,導函數的左極 限,導函數的右極 限。
二、羅爾定理
設函數f(x)在閉區間[a,b]上連續(其中a不等于b),在開區間(a,b)上可導,且f(a)=f(b),那么至少存在一點ξ∈(a、b),使得f‘(ξ)=0。羅爾定理是以法國數學家羅爾的名字命名的。羅爾定理的三個已知條件的意義,①f(x)在[a,b]上連續表明曲線連通端點在內是無縫隙的曲線;②f(x)在內(a,b)可導表明曲線y=f(x)在每一點處有切線存在;③f(a)=f(b)表明曲線的割線(直線AB)平行于x軸;羅爾定理的結論的直幾何意義是:在(a,b)內至少能找到一點ξ,使f’(ξ)=0,表明曲線上至少有一點的切線斜率為0,從而切線平行于割線AB,與x軸平行。
三、泰勒公式展開的應用專題
相信很多同學看到泰勒公式就哆嗦,因為乍一看很長很恐怖,瞬間大腦空白,身體失重的感覺。其實在搞明白以下幾點后,這樣的癥狀就能夠消失了。1.什么情況下要進行泰勒展開;2.以哪一點為中心進行展開;3.把誰展開;4.展開到幾階?
四、應用多次中值定理的專題:
大部分的考研數學題,一般要考察你應用多次中值定理,最重要的就是要培養自己對這種題目的敏感度,要很快反映老師出這題考哪幾個中值定理,敏感性是靠自己多練習綜合題培養出來的。比如經常去復習,那樣對中值定理的題目早已沒有那種剛學高數時的害怕之極。
五、對稱性,輪換性,奇偶性在積分(重積分,線,面積分)中的綜合應用:
這類考研數學題型幾乎每年必考,要么小題中考,要么大題中要用,這是必須掌握的知識,但是往往不是那么容易就靠做3,4個題目就能了解這知識點的應用到底有多廣泛。我們做積分題,尤其多重積分和線面積分,死算也許能算出結果,但是要是能用以上性質,那可真是三下五除二搞定,這方面的感覺相信大家有過,可是或許僅僅是曇花一現,因為你做出來了以為以后就一定會在相似的題目中用,其實不然,因為僅僅靠幾道題目很大程度上不能給你留下太深刻的印象,下次輪到的時候或許就是考場上了,你可能頓時苦思冥想,最終還是選擇了最傻的辦法,浪費了寶貴時間。說這些其實就是說明,考場上的正常或超常發揮是建立在平時踏實做,見識廣,嚴要求的基礎上。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
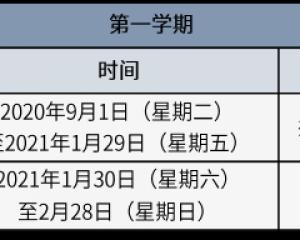 北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
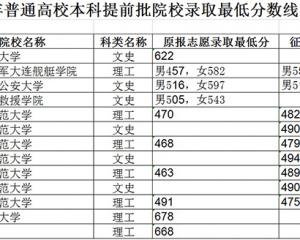 黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19
黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19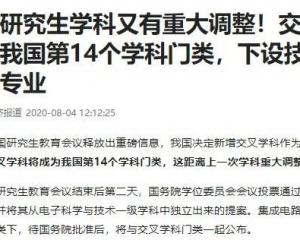 交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10
交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10 2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06
2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06